# Dr. M. Baron, Statistical Machine Learning class, STAT-427/627

# SUPPORT VECTOR MACHINES

1. SVM with various kernels

The SVM command is in package called e1071.

> install.packages("e1071");

> library(e1071)

Let’s use support vector machines to classify cars into Economy and Consuming classes.

> ECO = ifelse( mpg > 22.75, "Economy", "Consuming" )

> Color = ifelse( mpg > 22.75, "green", "red" )

> plot( weight, horsepower, lwd=3, col=Color )

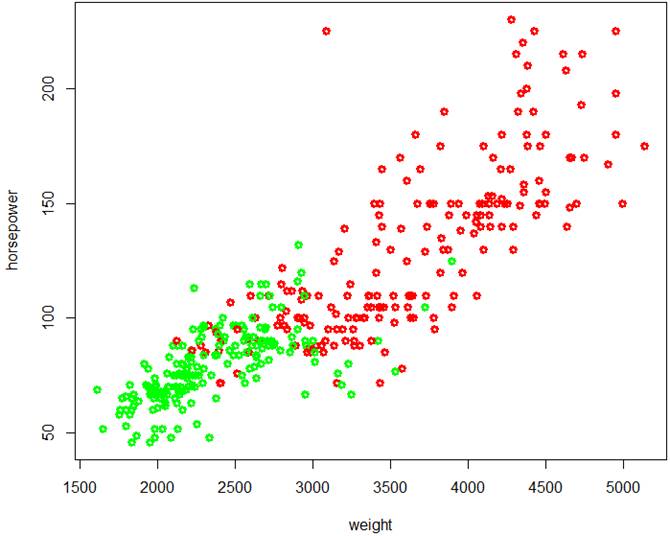
The two classes cannot be separated by a hyperplane, but the SVM method is surely applicable.

> S = svm( ECO ~ weight + horsepower, data=Auto, kernel = "linear" )

Error in svm.default(x, y, scale = scale, ..., na.action = na.action) :

Need numeric dependent variable for regression.

Error? There are other, unused variables in dataset Auto that prevent R from doing this SVM analysis. We’ll create a reduced dataset.

> d = data.frame(ECO, weight, horsepower)

> S = svm( ECO ~ weight + horsepower, data=d, kernel="linear" )

> summary(S)

Parameters:

SVM-Type: C-classification

SVM-Kernel: linear

cost: 1

gamma: 0.5

Number of Support Vectors: 120

( 60 60 )

So, there are 120 points violating the separating hyperplane or the margin, 60 in each class.

> plot(S, data=Auto)

Error in plot.svm(S, data = Auto) : missing formula.

Same story. We need to use a reduced dataset that contains only the needed variables.

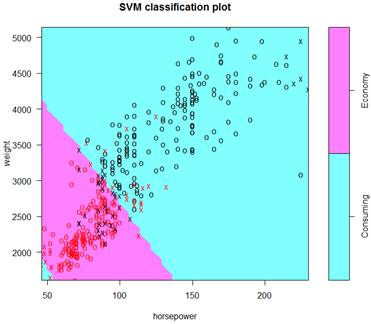
> plot(S, data=d)

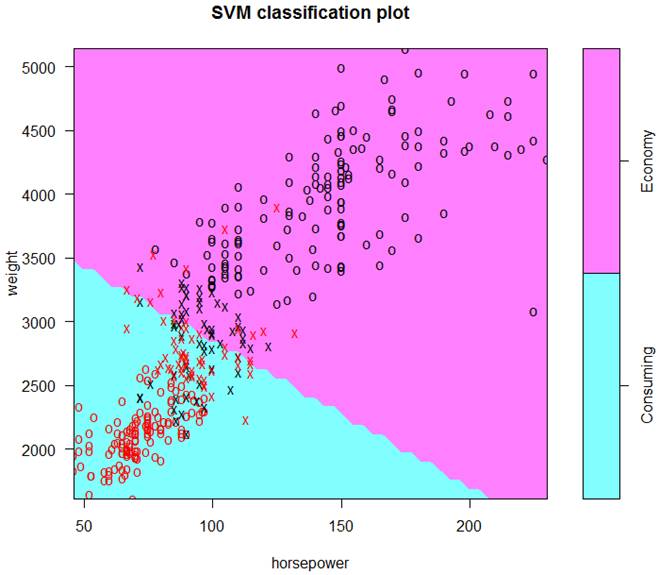
This is the final classification with a linear kernel and therefore, a linear boundary. Support vectors are marked as “x”, other points as “o”.

We can look at other types of kernels and boundaries – polynomial, radial, and sigmoid.

> S = svm( ECO ~ weight + horsepower, data=d, kernel="polynomial" )

> summary(S); plot(S,d)

Number of Support Vectors: 176

> S = svm( ECO ~ weight + horsepower, data=d, kernel="radial" )

> summary(S); plot(S,d)

Number of Support Vectors: 121

> S = svm( ECO ~ weight + horsepower, data=d, kernel="sigmoid" )

> summary(S); plot(S,d)

Number of Support Vectors: 74

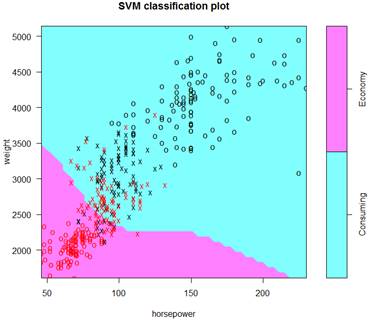
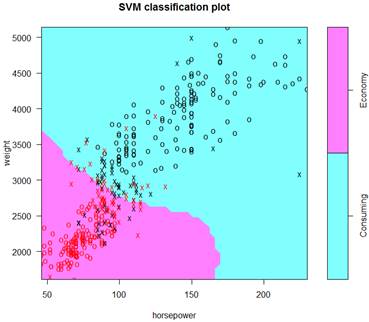
Adding more variables should give a better fit – to the training data.

> S = svm( factor(ECO) ~ weight + horsepower + displacement + cylinders, data=Auto, kernel="linear" )

> summary(S)

Number of Support Vectors: 99

We can identify the support vectors:

> S$index

[1] 16 17 18 25 33 45 46 48 60 61 71 76 77 78 80 100 107 108 109

[20] 110 111 112 113 119 120 123 153 154 162 173 178 199 206 208 209 210 240 241

[39] 242 253 258 262 269 273 274 275 280 281 384 24 31 49 84 101 114 122 131

[58] 149 170 177 179 192 205 218 233 266 270 271 296 297 298 299 305 306 313 314

[77] 318 322 326 327 331 337 338 353 355 356 357 358 360 363 365 368 369 375 381

[96] 382 383 385 387

> Auto[S$index,]

mpg cylinders displacement horsepower weight acceleration year origin

16 22.0 6 198 95 2833 15.5 70 1

17 18.0 6 199 97 2774 15.5 70 1

18 21.0 6 200 85 2587 16.0 70 1

25 21.0 6 199 90 2648 15.0 70 1

< truncated >

2. Tuning and cross-validation

The “cost” option specifies the cost of violating the margin. We can try costs 0.001, 0.01, 0.1, 1, 10, 100, 1000:

> Stuned = tune( svm, ECO ~ weight + horsepower, data=d, kernel="linear", ranges=list(cost=10^seq(-3,3)) )

> summary(Stuned)

- sampling method: 10-fold cross validation

- best parameters:

cost

0.1

- best performance: 0.1173718

- Detailed performance results:

cost error dispersion

1 1e-03 0.2478205 0.10663023

2 1e-02 0.1432051 0.05485355

3 1e-01 0.1173718 0.04208311 # This cost yielded the lowest cross-validation error of classification.

4 1e+00 0.1326282 0.04461101

5 1e+01 0.1351923 0.04819639

6 1e+02 0.1351923 0.04819639

7 1e+03 0.1351923 0.04819639

We can also find the optimal kernel.

> Stuned = tune( svm, ECO ~ weight + horsepower, data=d, ranges=list(cost=10^seq(-3,3), kernel=c("linear","polynomial","radial","sigmoid")) )

> summary(Stuned)

Parameter tuning of ‘svm’:

- sampling method: 10-fold cross validation

- best parameters:

cost kernel

0.1 sigmoid

- best performance: 0.1046154

- Detailed performance results:

cost kernel error dispersion

1 1e-03 linear 0.2164744 0.10501351

2 1e-02 linear 0.1326282 0.05074006

3 1e-01 linear 0.1096154 0.04330918

4 1e+00 linear 0.1172436 0.03813782

5 1e+01 linear 0.1223718 0.04775672

6 1e+02 linear 0.1223718 0.04775672

7 1e+03 linear 0.1223718 0.04775672

8 1e-03 polynomial 0.3720513 0.08274072

9 1e-02 polynomial 0.2601282 0.06438244

10 1e-01 polynomial 0.1987821 0.07443903

11 1e+00 polynomial 0.1784615 0.05328633

12 1e+01 polynomial 0.1580769 0.04909157

13 1e+02 polynomial 0.1555128 0.04999836

14 1e+03 polynomial 0.1504487 0.04722372

15 1e-03 radial 0.5816026 0.05687780

16 1e-02 radial 0.1301282 0.05190241

17 1e-01 radial 0.1198077 0.05104329

18 1e+00 radial 0.1223718 0.04118608

19 1e+01 radial 0.1096795 0.04835338

20 1e+02 radial 0.1198718 0.04184981

21 1e+03 radial 0.1146795 0.04354410

22 1e-03 sigmoid 0.5816026 0.05687780

23 1e-02 sigmoid 0.1530769 0.04517581

24 1e-01 sigmoid 0.1046154 0.03711533 # The best kernel and cost.

25 1e+00 sigmoid 0.1173718 0.04715638

26 1e+01 sigmoid 0.1530769 0.06159616

27 1e+02 sigmoid 0.1582051 0.06489946

28 1e+03 sigmoid 0.1582051 0.06489946

> Soptimal = svm( ECO ~ weight + horsepower, data=d, cost=0.1, kernel="sigmoid" )

> summary(Soptimal); plot(Soptimal,data=d)

Parameters:

SVM-Type: C-classification

SVM-Kernel: sigmoid

cost: 0.1

gamma: 0.5

Number of Support Vectors: 164 # We know that more support vectors imply a lower variance

( 82 82 )

Number of Classes: 2

Levels: Consuming Economy

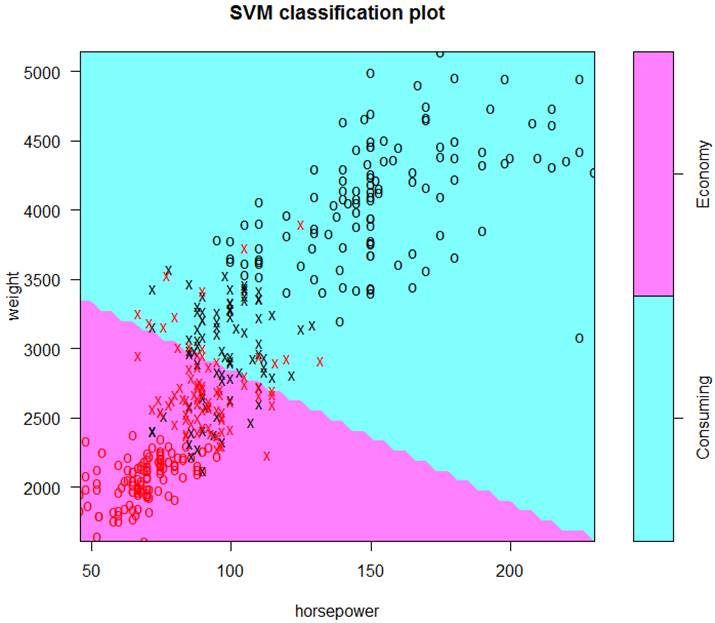
Let’s use the validation set method to estimate the classification rate of this optimal SVM.

> n = length(mpg); Z = sample(n,n/2)

> Strain = svm( ECO ~ weight + horsepower, data=d[Z,], cost=0.1, kernel="sigmoid" )

> Yhat = predict( Strain, data=d[-Z,] )

> table( Yhat, ECO[Z] )

Yhat Consuming Economy

Consuming 82 9

Economy 17 88

> table( Yhat, ECO[Z] )

> mean( Yhat==ECO[Z] )

[1] 0.8673469

3. More than two classes

Let’s create more categories of ECO. The same tool svm( ) can handle multiple classes.

> summary(mpg)

Min. 1st Qu. Median Mean 3rd Qu. Max.

9.00 17.00 22.75 23.45 29.00 46.60

> ECO4 = rep("Economy",n)

> ECO4[mpg < 29] = "Good"

> ECO4[mpg < 22.75] = "OK"

> ECO4[mpg < 17] = "Consuming"

> table(ECO4)

ECO4

Consuming Economy Good OK

92 103 93 104

> S4 = svm( ECO4 ~ weight + horsepower, data=d, cost=0.1, kernel="sigmoid" )

Error in svm.default(x, y, scale = scale, ..., na.action = na.action) :

Need numeric dependent variable for regression.

R was trying to do regression SVM but realized that ECO4 is not numerical. We can direct R to do classification by replacing ECO4 with factor(ECO4).

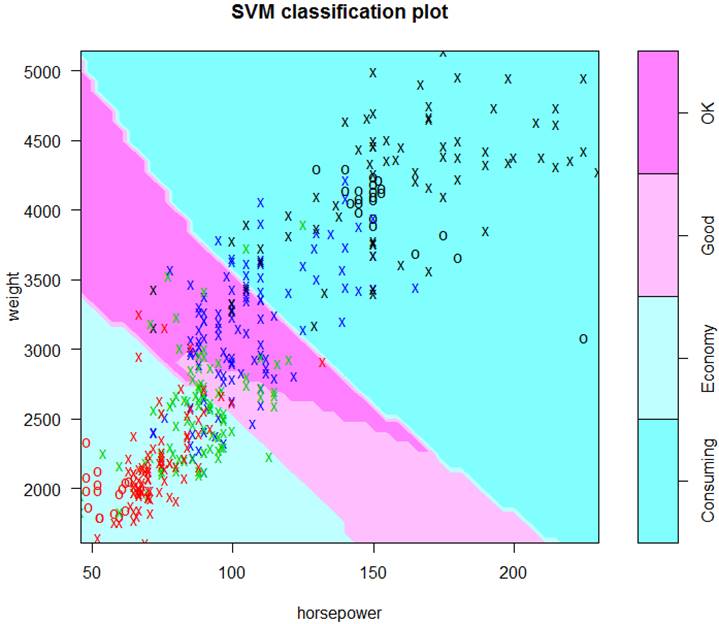
> S4 = svm( factor(ECO4) ~ weight + horsepower, data=d, cost=0.1, kernel="sigmoid" )

> plot(S4, data=d)

> Yhat = predict( S4, data.frame(Auto) )

> table( Yhat, ECO4 )

ECO4

Yhat Consuming Economy Good OK

Consuming 88 0 2 33

Economy 0 96 58 15

Good 0 2 9 5

OK 4 5 24 51

> mean( Yhat == ECO4 )

[1] 0.622449

It’s more difficult to predict finer classes correctly